Расчет характеристик синхронного трехфазного двигателя с многополюсным ротором на постоянных магнитах

Расчет характеристик синхронного трехфазного двигателя
с многополюсным ротором на постоянных магнитах

Появление высококоэрцитивных постоянных магнитов и, в особенности, редкоземельных магнитов с высокими значениями магнитной энергии позволяет в ряде случаев избавиться от токовых обмоток на роторе электрической машины без ухудшения ее характеристик. Электромашина с ротором на постоянных магнитах не имеет коллектора и щеток, что позволяет существенно повысить ее надежность и время работы без обслуживания и ремонта. Одной из частных задач является конструирование синхронных трехфазных исполнительных двигателей с многополюсным ротором, обладающих достаточно высоким значением момента на валу, что позволяет использовать их непосредственно в качестве привода, обходясь без редуктора.

Поперечное сечение двигателя показано на рис. 2.1.

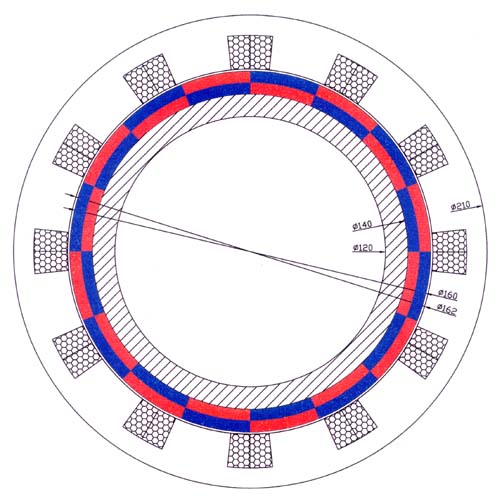
Рис. 2.1. Поперечное сечение синхронного трехфазного двигателя с 16-полюсным ротором на постоянных магнитах.

Двигатель состоит из ротора и статора. В конструкцию ротора входит стальной цилиндр (внешний диаметр 140 мм, толщина стенки 10 мм), на котором крепятся 16 постоянных магнитов состава неодим-железо-бор (Ne-Fe-B, остаточная индукция примерно 1.2 Тл, коэрцитивная сила по намагниченности примерно 1000 кА/м) в виде подковообразных сегментов высотой 10 мм с чередующимся направлением намагниченности. Внешний диаметр ротора 160 мм. Высота ротора 50 мм. Статор представляет собой стальной цилиндр (набран из листовой электротехнической стали) с 12-ю внутренними прорезями, в которые помещаются обмотки (3 фазы по 4 последовательно включенных обмотки в каждой фазе). Внутренний диаметр статора 162 мм. Внешний диаметр статора 210 мм. Высота статора 50 мм. Частота вращения двигателя до 1000 об./мин. Для управления двигателем используется трехфазная последовательность импульсов напряжения переменной полярности.

Расчет магнитной индукции и других связанных с ней параметров, в частности, статического момента, можно произвести методом конечных элементов [1 - 4]. На рис. 3.1 показано распределение магнитного поля в магнитной системе двигателя, причем ротор находится в положении, при котором направление тока в одной из фаз изменяется на противоположное. Плотность тока в каждой обмотке 3 А/мм². При факторе упаковки, равном 0.6, плотность тока в обмоточном проводе составит 5 А/мм².

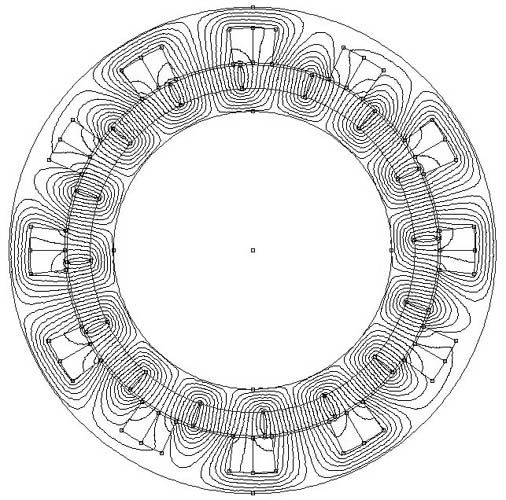
Рис. 3.1. Распределение магнитного поля в магнитной системе двигателя в момент переключения направления тока в одной из фаз. Плотность тока в каждой обмотке 3 А/мм².

Таблица 3.1. Зависимость статического момента от угла поворота ротора.

Угол поворота ротора, градусов	Статический момент при плотности тока в обмотке 3 А/мм², Н · м	Статический момент при плотности тока в обмотке 5 А/мм², Н · м
0 (момент переключения направления тока в обмотке)	25.57	42.48
1	26.28	44.83
2	30.67	50.54
3	33.20	53.55
4	29.87	50.25
5	27.43	46.95
6	29.23	47.82
7	27.51	45.09
7.5 (момент переключения направления тока в обмотке)	25.54	42.45

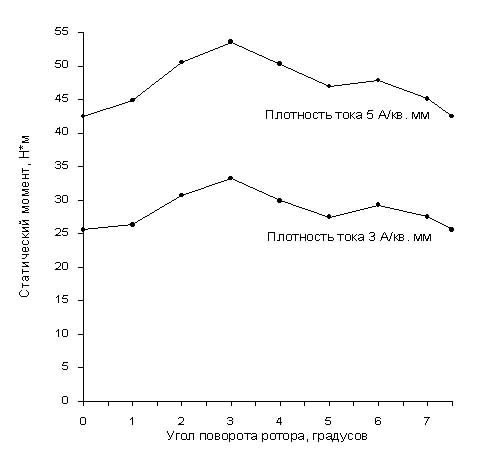
Рис. 3.2. График зависимости статического момента на валу двигателя от угла поворота ротора.

4. Расчет допустимой плотности тока в обмотках

Для провода с электрическим током удельная мощность P_V (мощность на единицу объема), рассеиваемая в проводе из-за наличия электрического сопротивления и превращающаяся в тепло, может быть найдена по формуле:

где r_E - удельное электрическое сопротивление токопроводящего материала провода, l - фактор упаковки. От плотности тока в обмотке j зависит мощность тепловыделения и, соответственно, температура обмотки. Эта температура не должна превышать максимально допустимой для данной марки провода. Расчет температуры внутри обмотки и допустимой плотности тока в обмотках можно произвести методом конечных элементов [1 - 4]. На рис. 4.1 показано распределение температуры по поперечному сечению двигателя.

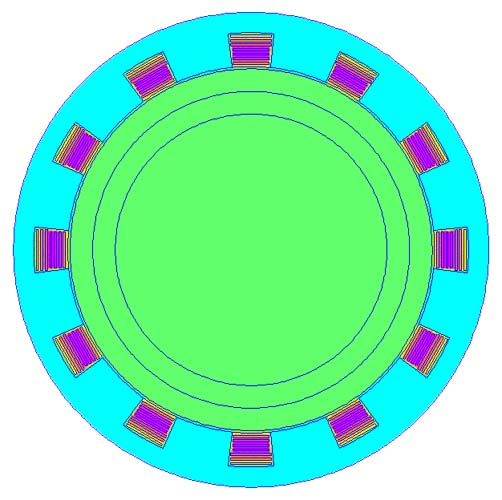
Рис. 4.1. Распределение температуры в двигателе в цветовой гамме (более высокая температура соответствует сдвигу в красную область спектра). Плотность тока в обмоточных проводах 5 А/мм². Фактор упаковки 0.6.

При плотности тока в обмоточном проводе, равной 5 А/мм² (если фактор упаковки равен 0.6, то плотность тока в самой обмотке будет 3 А/мм²), максимальный перегрев провода (превышение температуры провода над температурой окружающей двигатель воздушной среды) будет равен примерно 50 ⁰C.

При плотности тока в обмоточном проводе, равной 8.3 А/мм² (если фактор упаковки равен 0.6, то плотность тока в самой обмотке будет 5 А/мм²), максимальный перегрев провода будет равен примерно 120 ⁰C. При этом дополнительным фактором, который следует принять во внимание, является максимально допустимая рабочая температура постоянных магнитов, для Ne-Fe-B-магнитов равная примерно 100 ⁰C, поэтому может возникнуть необходимость принудительного охлаждения ротора двигателя.

5. Расчет активного сопротивления и индуктивности обмотки

Активное сопротивление R обмотки может быть найдено по формуле:

Здесь L_AV- длина средней линии обмотки, N – число витков, d – диаметр обмоточного провода.

Число витков N может быть выражено следующим образом:

Для расчета индуктивности обмотки L воспользуемся соотношением F = LI, где F – магнитный поток, пронизывающий обмотку, I – величина тока в обмоточном проводе:

Величину тока в обмоточном проводе можно найти таким образом:

Тогда получаем выражение для индуктивности обмотки:

Реактивное сопротивление обмотки Z_L на частоте f :

А полное сопротивление обмотки Z на частоте f:

Для двигателя вышеприведенной конструкции: L_AV = 0.2 м , S_W = 1.39 · 10^-4 м², F = 0.001 Вб при j = 3 А/мм², r_E = 1.67· 10^-8 Ом · м (обмотки намотаны медным проводом), l = 0.6 данные по расчетам активного сопротивления, индуктивности и реактивного сопротивления одной обмотки при частоте переключения тока 130 Гц (частота вращения ротора 1000 об./мин) в зависимости от диаметра обмоточного провода приведены в таблице:

Таблица 5.1. Зависимость активного, реактивного и полного сопротивления и индуктивности обмотки от диаметра обмоточного провода.

Диаметр обмоточного провода, мм	Активное сопротивление обмотки, Ом	Индуктивность обмотки, мГн	Реактивное сопротивление обмотки на частоте 130 Гц, Ом	Полное сопротивление обмотки на частоте 130 Гц, Ом
0.1	4516	25.46	20.80	4516
0.2	282.25	6.365	5.199	282.30
0.3	55.76	2.829	2.311	55.81
0.4	17.64	1.591	1.300	17.69
0.5	7.226	1.018	0.832	7.274
0.6	3.485	0.707	0.577	3.532
0.7	1.881	0.520	0.425	1.928
0.8	1.103	0.398	0.325	1.150
0.9	0.688	0.314	0.256	0.734
1.0	0.452	0.255	0.208	0.498
1.1	0.308	0.210	0.172	0.353
1.2	0.218	0.177	0.145	0.262
1.3	0.158	0.151	0.123	0.200
1.4	0.118	0.130	0.106	0.159
1.5	0.089	0.113	0.092	0.128
1.6	0.069	0.099	0.081	0.106

Диаметр обмоточного провода выбирается в зависимости от напряжения источника питания, прикладываемого к обмотке, таким образом, чтобы максимальная плотность тока в проводе не превышала значения, определяемого теплостойкостью изоляции (5 А/мм² для 100 ⁰C и 8.3 А/мм² для 160 ⁰C).

По вопросам расчета конкретных схем электрических двигателей обращайтесь к автору (см. раздел Контактная информация).