A_Magnet: Программа-калькулятор индукции магнитного поля
кольцевого (цилиндрического) магнита методом эквивалентного соленоида

Теория

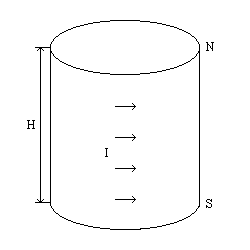
Рис. 1. Представление цилиндрического постоянного магнита эквивалентным соленоидом.

Постоянный магнит с аксиальным направлением намагниченности, в частности, цилиндрический, можно рассматривать как однослойный соленоид с бесконечно тонкой обмоткой, геометрически соответствующей боковой поверхности магнита, по которой течет намагничивающий ток I (см. рис. 1). Условием эквивалентности магнита и соленоида является равенство их магнитных моментов. Магнитный момент магнита (P) может быть найден по формуле:

P = M V = M S H, где M – намагниченность магнита, V – его объем, S – площадь сечения, H – высота.

Магнитный момент эквивалентного соленоида:

P = j H S, где j = I/H – линейная плотность намагничивающего тока.

Тогда:

j = M

Для материалов с прямоугольной петлей гистерезиса (феррит бария, феррит стронция, неодим-железо-бор, самарий-кобальт и т. п.):

M ~ Br/m₀, где Br – остаточная индукция, m₀ = 4p ∙ 10^-7 Гн/м – магнитная постоянная. Таким образом, линейную плотность намагничивающего тока можно выразить приближенной формулой:

j = Br/m₀

Кольцевой постоянный магнит с аксиальным направлением намагниченности может быть представлен как два однослойных цилиндрических соленоида с бесконечно тонкими обмотками, вложенные друг в друга. Соленоид диаметром D2 и высотой H соответствует внешней боковой поверхности магнита, а соленоид диаметром D1 и высотой H – внутренней поверхности отверстия. Намагничивающие токи в соленоидах равны по величине и противоположны по направлению.

Рассчитать величину и направление вектора магнитной индукции B в произвольной точке магнитного поля, создаваемого в вакууме (или воздухе) однослойным соленоидом с известной линейной плотностью тока, можно с помощью закона Био-Савара-Лапласа [2].

Программа Annular Magnet (A_Magnet)

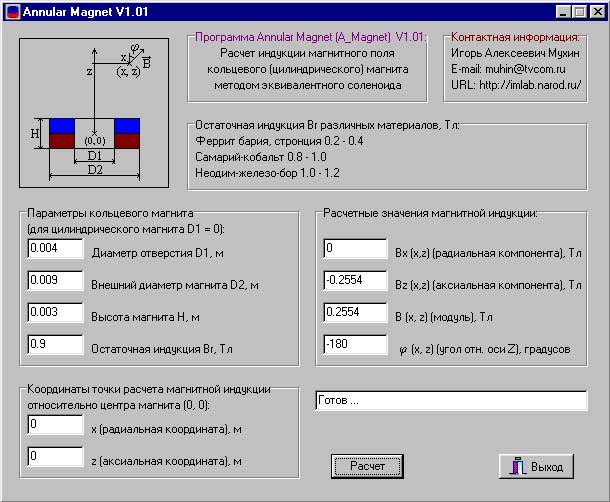
Рис. 2. Внешний вид окна программы A_Magnet (версия 1.01).

Входные данные:
D1 - диаметр отверстия магнита, м
D2 - внешний диаметр магнита, м
H - высота магнита, м
Br - остаточная индукция материала магнита, Тл
x - радиус точки (относительно точки (0, 0) - центра магнита), в которой требуется рассчитать составляющие магнитной индукции, м
z - высота точки (относительно точки (0, 0) - центра магнита), в которой требуется рассчитать составляющие магнитной индукции, м

Выходные данные:
Bx (x, z) - радиальная составляющая магнитной индукции в точке с координатами (x, z) (относительно точки (0, 0) - центра магнита), Тл
Bz (x, z) - аксиальная составляющая магнитной индукции в точке с координатами (x, z) (относительно точки (0, 0) - центра магнита), Тл
B - модуль магнитной индукции в точке с координатами (x, z) (относительно точки (0, 0) - центра магнита), Тл
f - угол между вектором магнитной индукции в точке с координатами (x, z) и осью Z, градусов

Программа A_Magnet позволяет рассчитывать по заданным геометрическим размерам (D1, D2, H) магнита и остаточной индукции (Br) материала, из которого сделан магнит, величину магнитной индукции (B, Bx, Bz) в заданной точке пространства (x, z). Расчеты производятся в системе СИ. Результаты выводятся на экран монитора.

Используя принцип суперпозиции [2], можно рассчитывать магнитные поля систем кольцевых (цилиндрических) постоянных магнитов.

Демонстрационная версия программы A_Magnet:

Версия 1.01: A_Magnet101d.rar (~88 Кбайт)

Демонстрационная версия программы позволяет рассчитывать индукцию магнитного поля на оси магнита (x = 0). Точность расчетов несколько ниже, чем в основной версии. Программа может работать с операционными системами (ОС) Windows 3.1, Windows 95, 98, XP и Vista (с другими ОС семейства Windows не проверялась).

Файл A_Magnet101d.rar необходимо распаковать в заранее созданную папку. Упаковка производилась с помощью WinRar 2.80. Результат распаковки: A_Magnet101d.exe - исполняемый файл программы. После запуска программы можно вводить входные данные и производить расчет нажатием соответствующей кнопки. Входные данные (D1 - диаметр отверстия, D2 - внешний диаметр магнита, H - высота магнита, x - радиальная координата (x = 0), z - аксиальная координата) необходимо вводить в метрах (учитывайте установленный в ОС формат разделителя для десятичной дроби - точка или запятая, например, 0.005 или 0,005; необходимо использовать тот разделитель, который установлен в ОС, в противном случае появится сообщение об ошибке). Остаточная индукция Br вводится в теслах. Проверить правильность расчетов можно по рис. 2.

Скопированные файлы могут быть проверены на отсутствие вирусного кода в режиме on-line [5].

По вопросу получения полной версии программы обращайтесь к автору (см. раздел Контактная информация).

Экспериментальная проверка программы

В качестве одного из примеров экспериментальной проверки программы A_Magnet на рис. 3 приведены результаты расчета и измерения [6] аксиальной составляющей магнитной индукции по оси постоянного цилиндрического магнита. Размеры магнита: диаметр 14.5 мм (D2 = 0.0145 м), высота 20 мм (H = 0.02 м). Состав: неодим-железо-бор, остаточная индукция ~1.1 Тл (Br = 1.1 Тл).

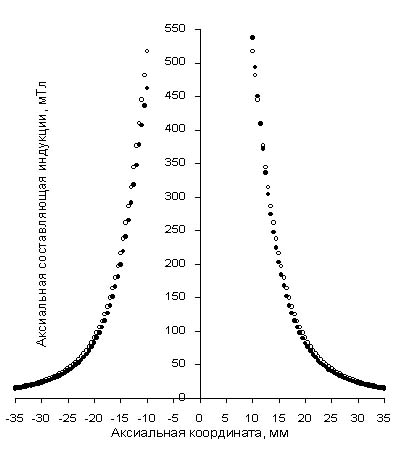
Рис. 2. Зависимость аксиальной составляющей магнитной индукции от аксиальной координаты: светлые кружки - расчетные значения, темные кружки - измеренные значения.

Некоторое расхождение измеренных и расчетных значений объясняется неоднородностью плотности постоянного магнита, возникающей вследствие особенностей технологии изготовления.

Ссылки:

1. Выгодский М. Я. Справочник по высшей математике. – М.: Издательство "Наука", гл. ред. физ.-мат. лит., 1977. – 872 с.; ил.
2. Законы и уравнения магнитного поля
3. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Издательство "Наука", гл. ред. физ.-мат. лит., 1968 г. – 720 с.; ил.
4. Постоянные магниты: Справочник / Альтман А. Б., Герберг А. Н., Гладышев П. А. и др.; Под ред. Ю. М. Пятина. - 2-е изд., перераб. и доп. - М.: Энергия, 1980. - 488 с., ил.
5. Проверка файлов пользователя на наличие вирусного кода в режиме on-line
6. Сканирование магнитных полей (магнитное сканирование)
7. Яворский Б. М., Детлаф А. А. Справочник по физике / Для инженеров и студентов вузов. – 7 изд., испр. – М.: Издательство "Наука", Гл. ред. физ.-мат лит., 1978. – 944 с.; ил.

Словарь терминов:

• Магнитная индукция - вектор, численно равный пределу отношения силы, действующей со стороны магнитного поля на элемент проводника с электрическим током, к произведению тока и длины элемента проводника, если длина этого элемента стремится к нулю, а элемент так расположен в поле, что этот предел имеет наибольшее значение, и направленный перпендикулярно к направлению элемента проводника и к направлению силы, действующей на этот элемент со стороны магнитного поля, причем из его конца вращение по кратчайшему расстоянию от направления силы к направлению тока в элементе проводника должно быть видно происходящим против часовой стрелки.
• Магнитное поле - разновидность электромагнитного поля, создаваемая движущимися электрическими зарядами или токами и оказывающая силовое воздействие на движущиеся электрические заряды или токи.
• Метод эквивалентного соленоида - расчетный метод, в основе которого лежит представление постоянного магнита с аксиальным направлением намагниченности в виде однослойного соленоида с бесконечно тонкой обмоткой, геометрически соответствующей боковой поверхности магнита, по которой течет намагничивающий ток такой величины, что магнитные моменты соленоида и магнита равны.
• Намагниченность – магнитный момент единицы объема.
• Операционная система (англ. operating system) - базовый набор программ, обеспечивающий работу компьютера и его взаимодействие с пользователем.
• Остаточная индукция - величина магнитной индукции, сохраняющейся в образце после уменьшения напряженности внешнего поля до нуля.
• Постоянный магнит - объект, создающий магнитное поле за счет собственных внутренних элементарных электрических токов, текущих без использования внешнего источника энергии в составляющем объект материале.
• Цилиндрический соленоид - соленоид в виде цилиндра с центральным цилиндрическим отверстием (если таковое имеется).

26.10.2005
02.11.2005
20.02.2006
17.02.2008

Альтернативные источники энергии
Компьютеры и Интернет
Магнитные поля
Механотронные системы
Перспективные разработки
Электроника и технология

Главная страница