M_Transducer: Программа расчета магнитоэлектрического преобразователя

1. Введение

Магнитоэлектрический преобразователь – преобразователь механического движения постоянного магнита относительно обмотки в электрический сигнал. Может либо выполнять функцию датчика скорости, либо использоваться в качестве электрогенератора. Основная задача - по заданным геометрическим и физическим параметрам системы необходимо рассчитать электродвижущую силу (ЭДС) на выходе.

2. Конструкция преобразователя

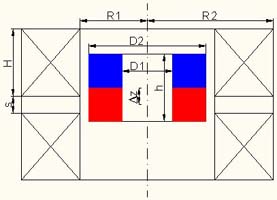
Рис. 2.1. Схема магнитоэлектрического преобразователя.

Постоянный магнит представляет собой кольцо (или цилиндр) внешним диаметром D2 высотой h с отверстием диаметром D1 (или без отверстия). Дифференциальный соленоид состоит из двух одинаковых цилиндрических соленоидов с радиусом отверстия R1 внешним радиусом R2 высотой H, намотанных проводом диаметром D с фактором упаковки l и разделенных прокладкой толщиной s. Расстояние между центрами дифференциального соленоида и магнита Dz (Delta z). Дифференциальный соленоид закреплен неподвижно. Осевая скорость магнита в заданной точке v.

3. Расчет индукции магнитного поля постоянного кольцевого (цилиндрического) магнита

Цилиндрический постоянный магнит  с аксиальным направлением намагниченности можно рассматривать как однослойный соленоид с бесконечно тонкой обмоткой, геометрически соответствующей боковой поверхности магнита, по которой течет намагничивающий ток I.

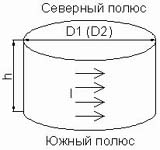
Рис. 3.1. Представление цилиндрического постоянного магнита эквивалентным соленоидом.

Условием эквивалентности магнита и соленоида является равенство их магнитных моментов. Магнитный момент магнита P может быть найден по формуле:

P = M V = M S h, где M – намагниченность магнита, V – его объем, S – площадь сечения, h – высота.

Магнитный момент эквивалентного соленоида:

P = j h S, где j = I/h – линейная плотность намагничивающего тока.

Тогда:

j = M

Для материалов с прямоугольной петлей гистерезиса (феррит бария, феррит стронция, неодим-железо-бор, самарий-кобальт и т. п.):

M ≈ Br/m₀, где Br – остаточная индукция, m₀ = 4p ∙ 10^-7 Гн/м – магнитная постоянная. Таким образом, линейную плотность намагничивающего тока можно выразить приближенной формулой:

j = Br/m₀

Кольцевой постоянный магнит с аксиальным направлением намагниченности может быть представлен как два однослойных цилиндрических соленоида с бесконечно тонкой обмоткой, вложенных друг в друга. Соленоид диаметром D2 и высотой h соответствует внешней боковой поверхности магнита, а соленоид диаметром D1 и высотой h – внутренней поверхности отверстия. Намагничивающие токи в соленоидах равны по величине и противоположны по направлению.

где dl – вектор элемента проводника, численно равный dl и проведенный в направлении тока, r – радиус-вектор, проведенный из этого элемента проводника в рассматриваемую точку поля, r = mod(r). Этот принцип положен в основу программы A_Magnet [1].

4. Расчет потокосцепления соленоида с магнитом и электродвижущей силы

Электродвижущая сила (ЭДС) E соленоида в соответствии с законом электромагнитной индукции Фарадея [6] может быть найдена по формуле:

где Y – потокосцепление соленоида с магнитным полем, t – время.

Формулу (4.1) можно записать в виде:

где z0 = H/2 + s/2 + Dz – расстояние между центрами магнита и соленоида, v – скорость движения магнита.

Дифференциальный соленоид состоит из двух одинаковых соленоидов. При последовательном электрическом и встречном магнитном включении соленоидов общая ЭДС равна сумме ЭДС каждого из соленоидов. Для одного соленоида z0 = H/2 + s/2 + Dz, для другого z0 = H/2 + s/2 – Dz.

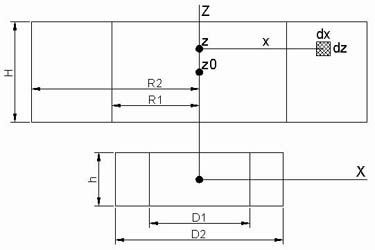
Рис. 4.1. К расчету потокосцепления магнита и соленоида.

Для расчета потокосцепления соленоид можно разбить на элементы прямоугольного сечения со сторонами dx ∙ dz (рис. 4.1), найти потокосцепление d² Y каждого такого элемента, а затем проинтегрировать по сечению обмотки.

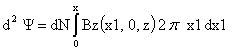
где Bz (x1, 0, z) - аксиальная (осевая) составляющая магнитной индукции поля магнита, dN – число витков обмоточного провода в элементе dx ∙ dz, выражаемое через фактор упаковки l и диаметр обмоточного провода D следующим образом:

Тогда:

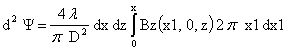
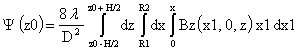
С учетом этого ЭДС может быть выражена таким образом:

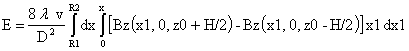
Тогда ЭДС E_DIF дифференциального соленоида:

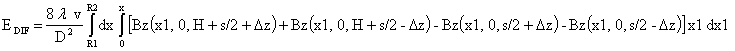
5. Расчет активного сопротивления и индуктивности дифференциального соленоида

Дифференциальный соленоид состоит из двух одинаковых цилиндрических соленоидов (рис. 5.1), каждый из которых может быть охарактеризован следующими параметрами:
R1 - внутренний радиус соленоида, м
R2 - внешний радиус соленоида, м
H - высота соленоида, м
D - диаметр обмоточного провода без изоляции (для проводов прямоугольного сечения производится пересчет по формуле D=(4S/p)^1/2, где S - площадь поперечного сечения провода, м²), м
Lambda = l - фактор упаковки (отношение площади, занятой проводом в поперечном сечении соленоида без учета изоляции, к площади поперечного сечения соленоида) [12].

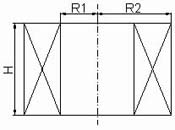
Рис. 5.1. Цилиндрический соленоид

Расчет активного сопротивления и индуктивности дифференциального соленоида может быть сделан с использованием решений, заложенных в программу Coil [2], и методики расчета индуктивности системы из двух соосных цилиндрических соленоидов [9].

6. Программа Magnetoelectric Transducer версия 1.0

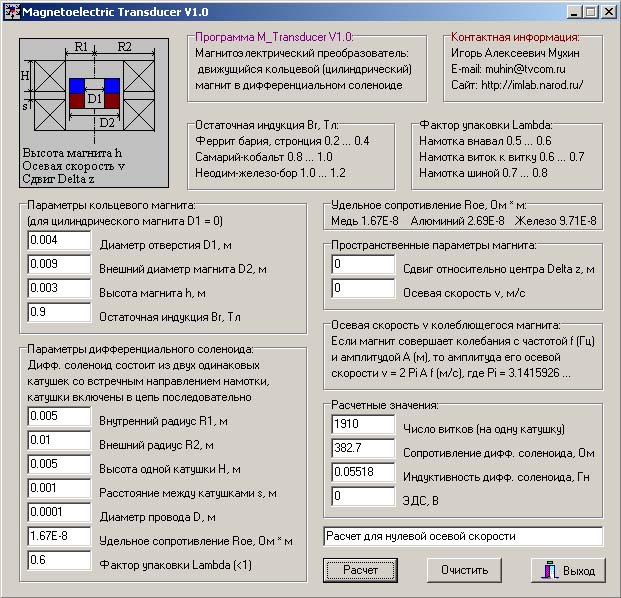
Рис. 6.1. Внешний вид окна программы Magnetoelectric Transducer (версия 1.0).

Входные данные:
D1 – диаметр отверстия в постоянном магните, м
D2 – внешний диаметр постоянного магнита, м
h – высота постоянного магнита, м
Br – остаточная индукция материала постоянного магнита, Тл
R1 – радиус отверстия в катушках дифференциального соленоида, м
R2 – внешний радиус катушек дифференциального соленоида, м
H - высота каждой из катушек дифференциального соленоида, м
s – расстояние между катушками дифференциального соленоида, м
D – диаметр обмоточного провода без изоляции (для проводов прямоугольного сечения производится пересчет по формуле D=(4S/p)^1/2, где S – площадь поперечного сечения провода, м²), м
re (Roe) – удельное электрическое сопротивление материала обмоточного провода, Ом ∙ м
l (Lambda) - фактор упаковки (отношение площади, занятой проводом в поперечном сечении соленоида без учета изоляции, к площади поперечного сечения соленоида)
Dz (Delta z) – сдвиг центра магнита относительно центра дифференциального соленоида, м
v – скорость движения магнита в осевом направлении, м/с

Если магнит совершает гармонические колебания в заданной точке (определяется параметром Delta z) с частотой f и амплитудой A, то амплитудное значение скорости в данной точке v определяется по формуле: v = 2 p A f.  При подстановке амплитудного значения скорости в программу можно произвести расчет амплитуды ЭДС для случая гармонических колебаний магнита.

Выходные данные:
Число витков одной катушки дифференциального соленоида
Активное сопротивление дифференциального соленоида (катушки соединены последовательно, условия нормальные), Ом
Индуктивность дифференциального соленоида (катушки соединены последовательно, направление намотки встречное), Гн
ЭДС на выходе дифференциального соленоида, В (амплитуда ЭДС для случая гармонических колебаний при использовании амплитудного значения скорости магнита)

Расчеты производятся в системе СИ. Результаты выводятся на экран монитора.

После запуска программы можно вводить входные данные и производить расчет нажатием кнопки "Расчет". Входные данные (D1, D2, h, Br, R1, R2, H, s, D, Roe, Lambda, Delta z и v) необходимо вводить, учитывая принятый в операционной системе (ОС) формат разделителя для десятичной дроби – точка или запятая, например, 0.005 или 0,005, либо установите в ОС точку в качестве разделителя. Для удельного сопротивления используется формат X.XXEY, где латинская буква E обозначает основание 10, а Y – степень (например, 1.67E-8 = 1.67 ∙ 10^-8 = 0.0000000167).

Для очистки окон с выходными данными следует нажать кнопку "Очистить". Для того, чтобы закрыть программу, следует нажать кнопку "Выход".

7. Демонстрационная версия программы M_Transducer:

Версия 1.0 демо: M_Transducer10d.rar (~81 Кбайт)

Демонстрационная версия программы позволяет рассчитывать параметры магнитоэлектрического преобразователя только для нулевой скорости движения магнита (v = 0). Время одного расчета может составлять до нескольких десятков секунд при использовании компьютера с процессором Pentium-I 200 МГц или аналогичным. Программа может работать с операционными системами (ОС) Windows 3.1, Windows 95, 98 и XP (с другими ОС семейства Windows не проверялась).

Файл M_Transducer10d.rar необходимо распаковать в заранее созданную папку. Упаковка производилась с помощью WinRAR 3.60. Результат распаковки: M_Transducer10d.exe - исполняемый файл программы. После запуска программы можно вводить входные данные в системе СИ и производить расчет нажатием соответствующей кнопки. Проверить правильность расчетов можно по внешнему виду окна программы, приведенному на рис. 6.1.

Скопированные файлы могут быть проверены на отсутствие вирусного кода в режиме on-line [11].

По вопросу получения полной версии программы обращайтесь к автору (см. раздел Контактная информация).

Ссылки:

1. A_Magnet: Программа-калькулятор индукции магнитного поля кольцевого (цилиндрического) магнита методом эквивалентного соленоида
2. Coil: Программа для расчета параметров и магнитного поля цилиндрического соленоида
3. Выгодский М. Я. Справочник по высшей математике. – М.: Издательство "Наука", гл. ред. физ.-мат. лит., 1977. – 872 с.; ил.
4. Гофман Ю. В. Законы, формулы, задачи физики. Справочник. – К., "Наук. думка", 1977. – 576 с.
5. Двайт Г. Б. Таблицы интегралов и другие математические формулы. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 176 с.
6. Законы и уравнения магнитного поля
7. Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей: Справочная книга. - 3-е изд., перераб. и доп. Л.: Энергоатомиздат. Ленингр. отд-ние, 1986. - 488 с.: ил.
8. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Издательство "Наука", гл. ред. физ.-мат. лит., 1968 г. – 720 с.; ил.
9. Методика расчета индуктивности системы из двух соосных цилиндрических соленоидов
10. Постоянные магниты: Справочник / Альтман А. Б., Герберг А. Н., Гладышев П. А. и др.; Под ред. Ю. М. Пятина. - 2-е изд., перераб. и доп. - М.: Энергия, 1980. - 488 с., ил.
11. Проверка файлов пользователя на наличие вирусного кода в режиме on-line
12. Расчет фактора упаковки при намотке соленоидов
13. Яворский Б. М., Детлаф А. А. Справочник по физике / Для инженеров и студентов вузов. – 7 изд., испр. – М.: Издательство "Наука", Гл. ред. физ.-мат лит., 1978. – 944 с.; ил.

Словарь терминов:

• Активное сопротивление - часть полного сопротивления, связанная с тепловыделением.
• Дифференциальный соленоид - соленоид, состоящий из двух одинаковых соленоидов, расположенных соосно вблизи друг от друга и включенных встречно.
• Индуктивность - величина, численно равная потоку самоиндукции контура при токе единичной силы.
• Магнитная индукция - вектор, численно равный пределу отношения силы, действующей со стороны магнитного поля на элемент проводника с электрическим током, к произведению тока и длины элемента проводника, если длина этого элемента стремится к нулю, а элемент так расположен в поле, что этот предел имеет наибольшее значение, и направленный перпендикулярно к направлению элемента проводника и к направлению силы, действующей на этот элемент со стороны магнитного поля, причем из его конца вращение по кратчайшему расстоянию от направления силы к направлению тока в элементе проводника должно быть видно происходящим против часовой стрелки.
• Магнитное поле - разновидность электромагнитного поля, создаваемая движущимися электрическими зарядами или токами и оказывающая силовое воздействие на движущиеся электрические заряды или токи.
• Магнитоэлектрический преобразователь – преобразователь механического движения постоянного магнита относительно обмотки в электрический сигнал.
• Намагниченность – магнитный момент единицы объема.
• Операционная система (англ. operating system) - базовый набор программ, обеспечивающий работу компьютера и его взаимодействие с пользователем.
• Остаточная индукция - величина магнитной индукции, сохраняющейся в образце после уменьшения напряженности внешнего поля до нуля.
• Постоянный магнит - объект, создающий магнитное поле за счет собственных внутренних элементарных электрических токов, текущих без использования внешнего источника энергии в составляющем объект материале.
• Цилиндрический соленоид - соленоид в виде цилиндра с центральным цилиндрическим отверстием (если таковое имеется).

30.03.2012

Альтернативные источники энергии
Компьютеры и Интернет
Магнитные поля
Механотронные системы
Перспективные разработки
Электроника и технология

Главная страница